目录[-]
数据挖掘中经常需要度量样本的相似度或距离,来评价样本间的相似性。特征数据不同,度量方法也不相同。
欧式距离
欧式距离(Euclidean Distance)在数学上表示n维空间中两个点的直线距离。
- 计算公式
空间中两个点 $x=(x_1,\ldots,x_n)$ 和 $y=(y_1, \ldots,y_n)$ 的欧式距离为:
$$d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2}=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}$$
例如二维平面上两点 $a(x_1,y_1),b(x_2,y_2)$ 的欧式距离为:
$$d_{ab}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$$
曼哈顿距离
曼哈顿距离(Manhattan Distance)又称城市街区距离,用于表明两个坐标点在标准坐标系中的绝对轴距总和,也就是在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如百度百科上的例子:
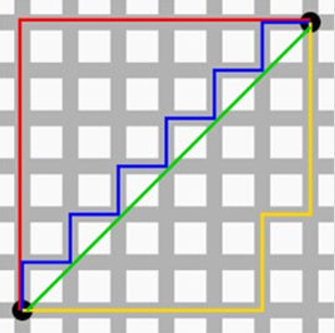
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。
- 计算公式
$n$ 维空间两点 $a(x_{11},\ldots,x_{1k})$ 和 $b(y_{21},\ldots,y_{2k})$ 间的曼哈顿距离为:
$$d_{ab}=\sum_{i=1}^k|x_{1i}-y_{2i}|$$
例如二维平面上两点 $a(x_1,y_1),b(x_2,y_2)$ 的曼哈顿距离为:
$$d_{ab}=|x_1-x_2|+|y_1-y_2|$$
切比雪夫距离
切比雪夫距离(Chebyshev Distance)在数学上,是 $L_{\infty}$ 度量,是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值。
- 计算公式
$n$ 维空间两点 $a(x_{11},\ldots,x_{1k})$ 和 $b(y_{21},\ldots,y_{2k})$ 间的切比雪夫距离为:
$$d_{ab}=max_i(|x_{1i}-y_{2i}|)$$
例如二维平面上两点 $a(x_1,y_1),b(x_2,y_2)$ 的切比雪夫距离为:
$$d_{ab}=max(|x_{1}-y_{1}|,|x_{2}-y_{2}|)$$
闵式距离
闵式距离(Minkowski Distance)又叫做闵可夫斯基距离,它不是一种距离,而是一组距离的定义。被看做是欧氏距离和曼哈顿距离的一种推广。
- 定义
对于 $n$ 维空间两点 $a(x_{11},\ldots,x_{1n})$ 和 $b(y_{21},\ldots,y_{2n}) \in R^n$ 间的闵式距离定义为:
$$d_{ab}=(\sum_{i=1}^n|x_{1i}-x_{2i}|^p)^{1 \over p}$$
其中 $p$ 是一个参数。 当 $p=1$ 时,就是曼哈顿距离; 当 $p=2$ 时,就是欧氏距离; 当 $p \rightarrow \infty$ 时,就是切比雪夫距离。 根据变参数的不同,闵氏距离可以表示一类的距离。
马氏距离
马氏距离(Mahalanobis Distance)表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。
马氏距离有很多优点,马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。它的缺点是夸大了变化微小的变量的作用。
- 计算公式
有向量$(\mu_1,\mu_2,\mu_3,\ldots,\mu_p)^T$ 均值为 $\mu$ ,协方差矩阵为 $\Sigma$ 。样本向量 $x=(x_1,x_2,x_3,\ldots,x_p)^T$ 到 $\mu$ 的马氏距离科表示为: $$D(x)=\sqrt{(x-\mu)^T\Sigma^{-1}(x-\mu)}$$
向量 $X_i$ 与 $X_j$ 的马氏距离定义为: $$D(X_i,X_j)=\sqrt{(X_i-X_j)^T\Sigma^{-1}(X_i-X_j)}$$
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则 $X_i$ 与 $X_j$ 之间的马氏距离等于他们的欧氏距离: $$D(X_i,X_j)=\sqrt{(X_i-X_j)^T(X_i-X_j)}$$
若协方差矩阵是对角矩阵,则就是标准化欧氏距离。
汉明距离
汉明距离(Hamming Distance)在信息论中表示两个等长字符串之间对应位置的不同字符串个数。换而言之,就是将一个字符串变换成另一个等长字符串所需要的 替换 次数。
汉明重量:是字符串相对于同样长度的零字符串的汉明距离,也就是说,它是字符串中非零的元素个数:对于二进制字符串来说,就是1的个数,所以11101的汉明重量是4。因此,如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。
编辑距离,又称Levenshtein距离(也叫做Edit Distance),是汉明距离的一般化,指两个字串之间,由一个转成另一个所需的最少编辑操作次数,如果它们的距离越大,说明它们越是不同。许可的编辑操作包括替换、插入、删除。
杰卡德距离
杰卡德相似系数(Jaccard similarity coefficient) 表示两个集合 $A$ 和 $B$ 的交集与并集的比值,是衡量两个集合相似度的一种指标。 $$J(A,B)=\frac{|A \bigcap B|}{|A \bigcup B|}$$
杰卡德距离(Jaccard Distance)是与杰卡德相似系数相反的概念。用来衡量两个集合差异性的一种指标。杰卡德距离可用如下公式表示: $$D_j(A,B)=1-J(A,B)=\frac{|A \bigcup B| - |A \bigcap B|}{|A \bigcup B|}$$
相关距离
皮尔森相关系数(Pearson correlation coefficient),相关系数有很多种,这里以常用的P相关系数为例。P相关系数是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高。当X与Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关)。
- 定义
$$\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}=\frac{\sum_{i=1}^n(X_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_{i=1}^n(X_i-\overline{x})^2\sqrt{\sum_{i=1}^n(y_i-\overline{y})^2}}}$$
相关距离: $$D_{xy}=1-{\rho}_{xy}$$
余弦距离
几何中,夹角余弦可用来衡量两个向量方向的差异;通过测量两个向量的夹角的余弦值来度量它们之间的相似性。两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。这结果是与向量的长度无关的,仅仅与向量的指向方向相关。余弦相似度通常用于正空间,因此给出的值为0到1之间。
- 定义
给定两个向量 A 和 B, 其余弦相似性 $\theta$ 的计算公式如下:
$$\cos(\theta)=\frac{A \cdot B}{\mid A\mid\mid B\mid}=\frac{\sum_{i=1}^nA_i \times B_i}{\sqrt{\sum_{i=1}^n(A_i)^2 \times \sqrt{\sum_{i=1}^n(B_i)^2}}}$$
例如,二维空间向量 $A(x_1,y_1)$ 和 $B(x_2,y_2)$ 的夹角余弦: $$\cos(\theta)=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}$$
信息熵
信息熵(Information Entropy)描述的是整个系统内部样本之间的一个距离,或者称之为系统内样本分布的集中程度(一致程度)、分散程度、混乱程度(不一致程度)。系统内样本分布越分散(或者说分布越平均),信息熵就越大。分布越有序(或者说分布越集中),信息熵就越小。
- 定义
计算给定的样本集 X 的信息熵的公式:
$$Entropy(X)=-\sum_{i=1}^np_i \log_2p_i$$
参数含义: $n$:样本集 $X$ 的分类数; $p_i$: $X$ 中第 $i$ 类出现的概率。
信息熵越大表明样本集X的分布越分散(分布均衡),信息熵越小则表明样本集X的分布越集中(分布不均衡)。当X中n个分类出现的概率一样大时(都是1/n),信息熵取最大值log2(n)。当X只有一个分类时,信息熵取最小值0。
